Differential Equations

Any equations that contains derivatives (ordinary or partial)

Order : Largest derivative presents
Linear : Linear combination of function y(t) and its derivatives
Initial Value Problem (IVP) : D.E. along with a set of initial conditions
General solution : The most general form of the solution without taking into account any initial conditions
Actual solution : Specific solution that satisfies both D.E. and Initial conditions.
Modeling : The process of describing a physical phenomenon as a D.E.

Direction Fields

1. Sketch of solutions. Since the arrows in the direction fields are in fact tangents to the actual solutions to the differential equations we can use these as guides to sketch the graphs of solutions to the differential equation.
2. Long Term Behavior. In many cases we are less interested in the actual solutions to the differential equations as we are in how the solutions behave as t increases. Direction fields can be used to find information about this long term behavior of the solution.
3. See dependancy on initial conditions

family of solution curves or integral curves : graphed set of solutions (blue lines)

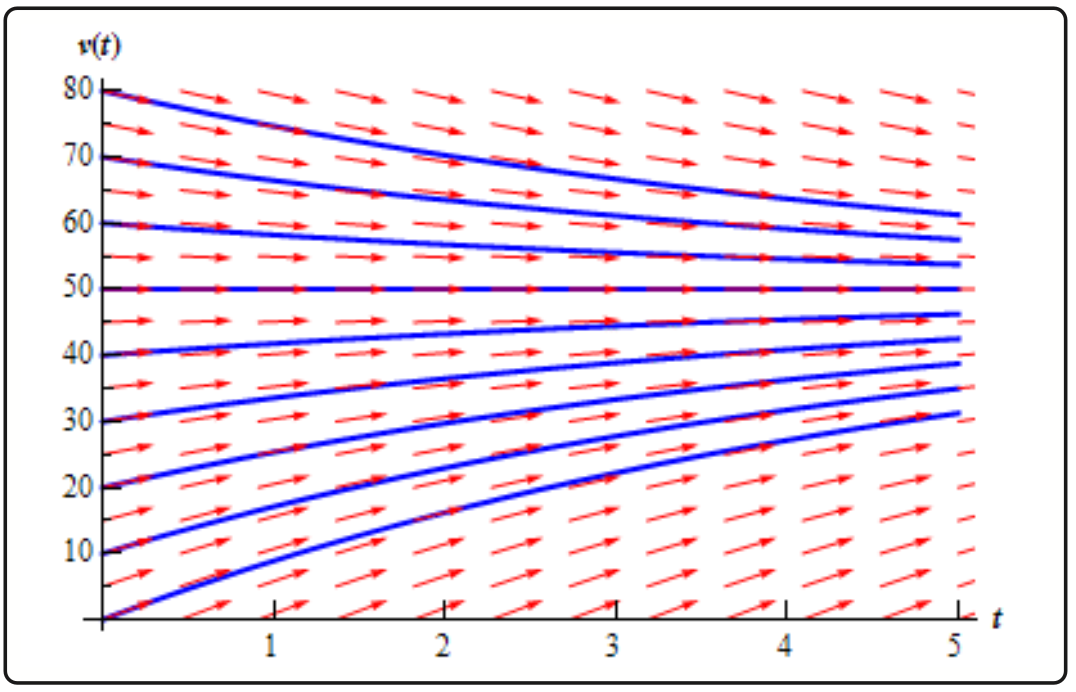
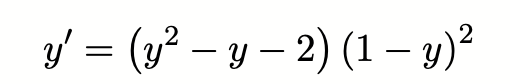
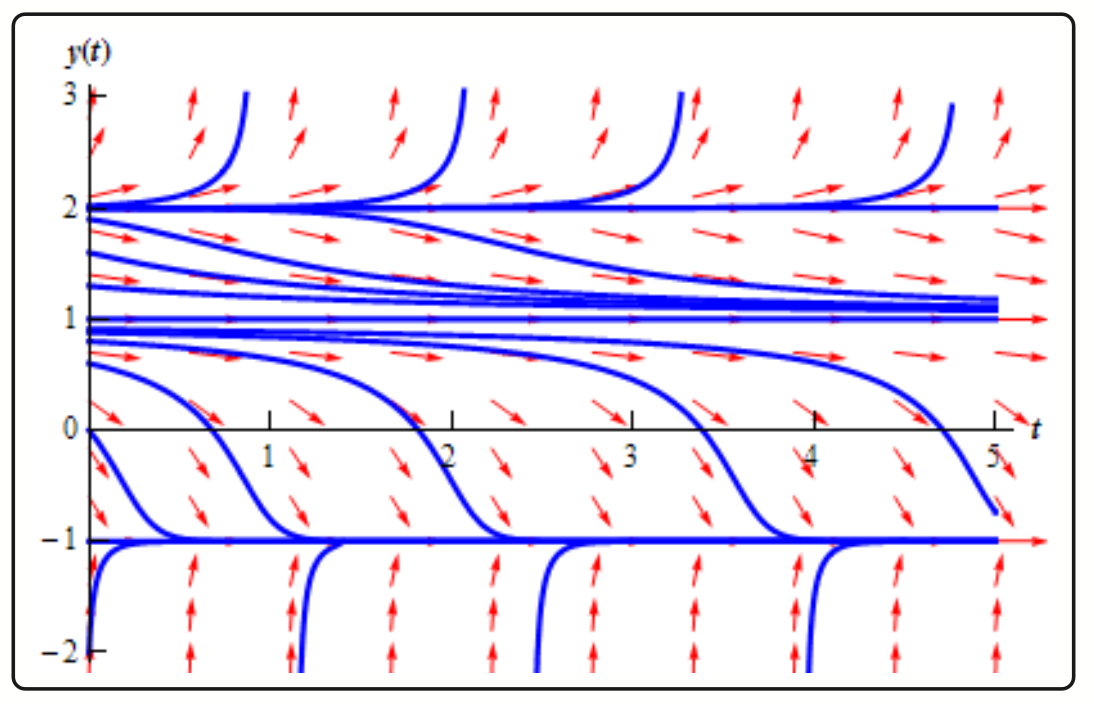
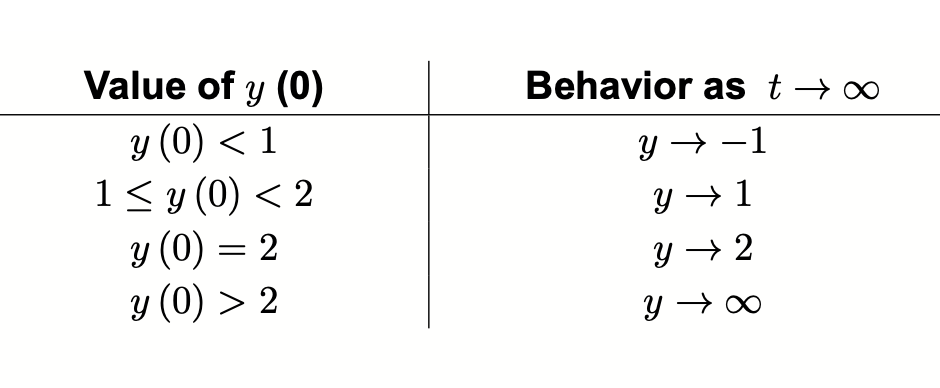
Equilibrium points - dependancy on initial conditions

Uniqueness question : Solving a D.E. with initial conditions should give us one unique solution
If a D.E. has as solution can we find it?

We are going to examine various cases of D.E. by their order:

1. First order Differential Equations
2. Second Order Differential Equations