Newton's 1st Law

A point object subject to zero net force moves in a straight line with constant speed (does not accelerate)
This is only true in inertial frames. Newton's 1st law is used as a definition of inertial frames.

Galilean transformation

Suppose that we have an inertial frame of reference. Let us set up a Cartesian coordinate system in this frame. A second frame of reference moving with a constant velocity u relative to the first frame. Without loss of generality suppose : u=ux.
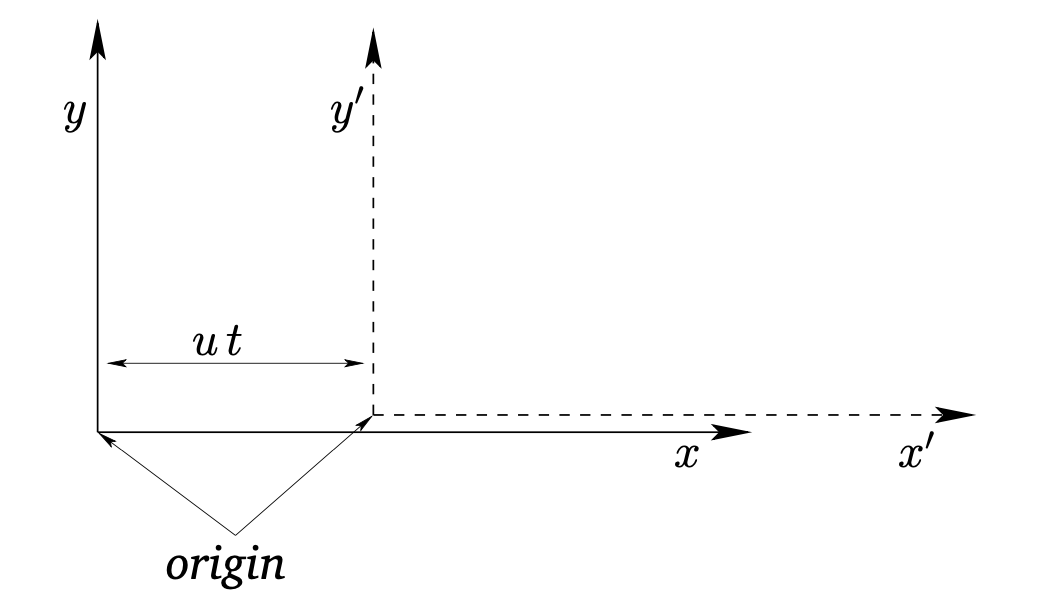
Pasted image 20240423130157.png|400

x^{'} = x - u t

y^{'} = y

z^{'} = z

v^{'} = v - u

By definition:

a^{'} = \frac{d v}{d t} = a

Conclusion

If an object is moving in a straight line with constant speed in our original inertial frame (i.e., if a = 0) then it also moves in a (different) straight-line with (a different) constant speed in the second frame of reference (i.e., a′ = 0). Hence, we conclude that the second frame of reference is also an inertial frame.

Newton thought that one of these inertial frames were special and defined an absolute standard of rest. Einstein showed that there is no such absolute standard of rest - all motion is relative (Relativity).

What if the second frame accelerates (a ≠ 0) ?

a^{'} = a - \frac{d u}{d t}

If an object is moving in a straight-line with constant speed in the first frame (i.e., if a = 0) then it does not move in a straight-line with constant speed in the second frame (i.e., a′ ≠ 0). Hence, if the first frame is an inertial frame then the second is not.

Conclusion

Any frame of reference which accelerates with respect to a given inertial frame is not itself an inertial frame.

Inertial frames

When studying the motions of objects in orbit around the Earth, a reference frame whose origin is the center of the Earth, and whose coordinate axes are fixed with respect to distant stars, is approximately inertial (ECEF ICRF). However, if such orbits are measured to extremely high precision then they will again be found to deviate very slightly from the predictions of Newtonian mechanics. In this case, the deviation is due to the Earth’s orbital motion about the Sun.

It is impossible to identify an absolute inertial frame—the best approximation to such a frame would be one in which the cosmic microwave background appears to be (approximately) isotropic. However, for a given dynamical problem, it is always possible to identify an approximate inertial frame. Any deviations of such a frame from a true inertial frame can be incorporated into the framework of Newtonian mechanics via the introduction of so-called fictitious forces.