Potential Energy

Potential energy: Energy the object has by virtue of its position.

Suppose particle with mass m moving in 1 dimension under conservative force ex. gravity.
Due to Stokes theorem:

F (x) = - \frac{d U (x)}{d x}

where U(x) is the Potential Energy of the particle.
Conservation of Energy (Newton's 2nd Law) :

K = E - U

and Kinetic Energy is always positive, meaning that U (and therefore the position) is always constrained :

U < E

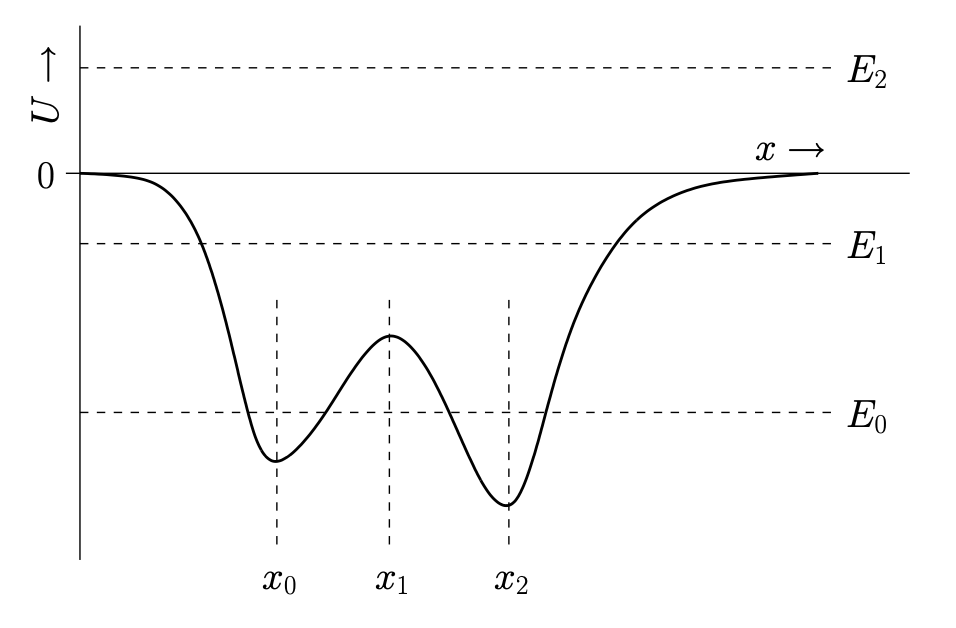
Pasted image 20240425174801.png|300
The particle is trapped in potential wells (ref Potential box) depending on the Energy of the motion.
On the above potential energy curve, if the total energy of the system is :

$E_{0}$ : The particle is trapped on one of the two wells
$E_{1}$ : The particle is bound, but can move freely between the two wells.
$E_{3}$ : The particle is unbound
In conservative systems in which it makes sense to adopt the convention that the potential energy at infinity is zero, bounded systems are characterized by E < 0, whereas unbounded systems are characterized by E > 0.

Equilibrium states are characterized by F=0 :

\frac{d U}{d t} = 0

Stable equilibrium points:
Small perturbation on stable equilibrium point => Harmonic Oscillator

\frac{d^{2} U}{d t^{2}} > 0

Unstable equilibrium points:
Small perturbation on unstable equilibrium point => exponential

\frac{d^{2} U}{d t^{2}} < 0

Neutral equilibrium points:

\frac{d^{2} U}{d t^{2}} = 0

Βαρυτική δυναμική ενέργεια αστέρα

Βαροτροπικό - Μάζα ενός φλοιού:

d m = 4 π r^{2} * ρ (r) d r

Δυναμική :

d W = - \frac{G m (r)}{r} d m (r)

Ομογενής αστέρας

ρ = σταθ
P = P(ρ)

W = - \frac{3}{5} \frac{G M^{2}}{R}

όπου

M = \frac{4 π}{3} ρ R^{3}