Coordinate transformation from GSE to SXI

Numerical - vector approach

Spherical -> cartesian GSE -> cartesian Satellite -> FOV elevation-azimuth

Find φ,θ from Numerical Solution & Performance for a set of $a$ and $r_{0}$ of the Shue model
Convert it to GSE cartesian through Geocentric Solar Ecliptic System tranformation
Convert to Satellite frame through the position and attitude files of the satellite:
The attitude is given through the definition of each base vector of the satellite in the GSE frame. We can the construct the rotation matrix from satellite to GSE: $R = [\begin{matrix} | & | & | \\ e_{x}^{s a t} & e_{y}^{s a t} & e_{z}^{s a t} \\ | & | & | \end{matrix}]$ And the relation between a vector in the GSE frame and the same vector in the satellite frame is ${\vec{v}}_{G S E} = R \cdot {\vec{v}}_{s a t} + \vec{t}$ where t is the translatithon vector (position of the satellite).
Therefore, the conversion from GSE to Satellite is defined: ${\vec{v}}_{s a t} = R^{⊤} \cdot ({\vec{v}}_{G S E} - \vec{t})$ This returns the tangent curve in the satellite frame:
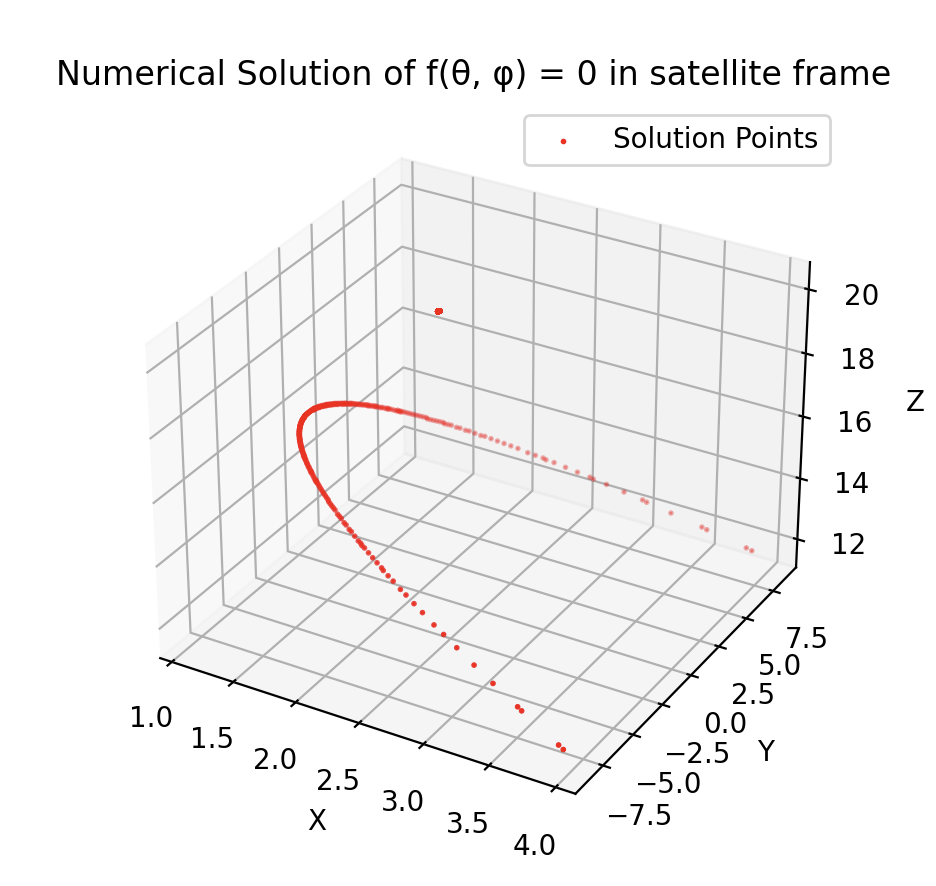
In order to project this in the FOV coordinates we need to compute the angle of each point from the z axis (boresight) along the x and y direction of the satellite frame: $a z i m u t h = \arctan \frac{x}{z}$ $e l e v a t i o n = \arctan \frac{y}{z}$

Spherical to spherical coordinates
From Tangent points to SXI in GSE we have the positions of the parametric tangent curve in the GSE:

F (θ, ϕ, r_{0}, a) = 0

We need to convert this to elevation and angle on the SXI FOV. For this we need:

If the origin of your new spherical system is shifted by ( $Δ r, Δ θ, Δ ϕ$ ), the new radial distance is:

r' = \sqrt{r^{2} + Δ r^{2} - 2 r Δ r \cos θ}

The new polar angle (relative to the shifted origin) is:

θ'_{translated} = \arccos (\frac{r \cos θ - Δ r}{r'})

And the azimuthal angle (after translation) is:

ϕ'_{translated} = ϕ + Δ ϕ

Now, let’s apply an Euler rotation defined by ( $α, β, γ$ ), assuming:

$α$ rotates about the x-axis (affecting $θ$ ).
$β$ rotates about the new y-axis
$γ$ rotates about the new z-axis (affecting $ϕ$ ).
Using a direct spherical rotation without converting to Cartesian:

\cos θ'' = \cos β \cos θ' translated + \sin β \sin θ' translated \cos (ϕ - α)

\sin θ'' \cos ϕ'' = \cos β \sin θ' translated \cos (ϕ - α) - \sin β \cos θ' translated

\sin θ'' \sin ϕ'' = \sin θ'_{translated} \sin (ϕ - α)

Depending on how we have defined the new axis and the corresponding rotation:

x = c o s θ

y = r s i n θ c o s ϕ

z = r s i n θ s i n ϕ

We can now take the projection in the XY plane to approximate the flat image plane and the corresponding parametric equation in this plane.